반응형

회귀분석 - Regression Analysis
회귀분석
회귀분석은 통계학의 가장 기초가 되는 알고리즘이자 중요한 기둥입니다. 회귀분석을 잘 이해한다면, 다른 심화 알고리즘의 이해에도 큰 도움이 될 것입니다.
회귀분석은 간단히 말해 종속변수와 하나 이상의 독립변수 간의 관계를 추정하는 것입니다. 영향을 미치는 변수 또는 영향이 없는 변수 등을 판단하고, 얼마나 영향을 미치는지에 따라 가중치를 산출하여 종속변수 예측에 활용합니다. 결국, 회귀분석의 최종 목표는 종속변수와 독립변수의 관계를 모델링하고 분석하여 예측을 하거나, 관계를 추론하거나, 독립변수의 변화가 종속변수에 어떻게 영향을 미치는지 이해하는 것입니다.
회귀분석 종류
회귀분석은 기준에 따라 여러가지로 분류할 수 있습니다. 데이터에 따라 알맞은 모형을 선택하여 적용하면 예측의 정확도는 향상됩니다. 분류 내용은 다음과 같습니다.
독립변수의 수에 따른 분류
| 구분 | 단순 회귀분석 Simple Regression |
다중 회귀분석 Multi Regression |
| 독립변수 개수 | 1개 | 2개 이상 |
독립변수와 종속변수의 관계 형태에 따른 분류
| 구분 | 선형 회귀분석 Linear Regression |
비선형 회귀분석 Nonlinear Regression |
다항 회귀분석 Polynomial Regression |
| 독립변수와 종속변수의 관계 |
 선형 |
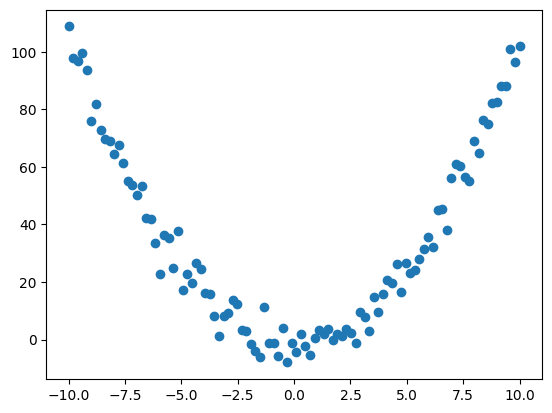 비선형 |
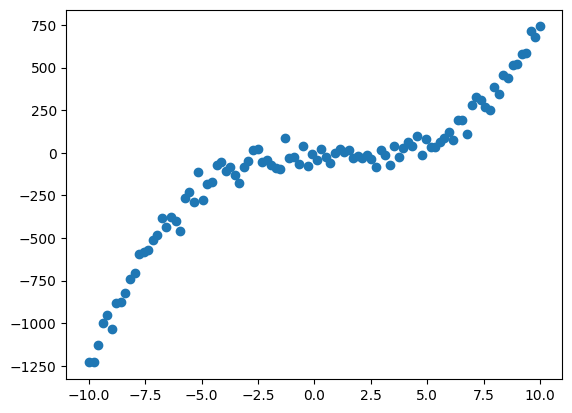 곡선 형태 |
반응형
종속변수의 성격에 따른 분류
- 로지스틱 회귀분석 Logistic Regression:
종속변수가 범주형 변수(이진형, 다중 클래스)일 때 사용 - 포아송 회귀분석 Poisson Regression:
종속변수가 음이 아닌 정수(ex. 사건 발생 횟수)일 때 사용 - 프로빗 회귀분석 Probit Regression:
누적 정규 분포함수를 사용하여 확률을 모델링
회귀 계수 추정 방법에 따른 분류
- 최소제곱법 회귀분석 Ordinary Least Squares, OLS:
가장 널리 사용되는 방법으로, 잔차 제곱합을 최소화하는 방법 - 능형 회귀분석 Ridge Regression:
다중공선성 문제를 해결하기 위해, 회귀 계수의 크기에 페널티를 추가하는 방법
(계수의 크기만 줄이고 0으로 만들지는 않음) - 라쏘 회귀분석 Lasso Regression:
불필요한 변수를 제거. 페널티 항에 절대값을 추가해 회귀 계수 중 일부를 0으로 만들 수 있음 - 엘라스틱넷 회귀분석 Elastic Net Regression:
Ridge와 Lasso 회귀의 장점을 결합한 방식. 두 페널티를 함께 사용하여 회귀 계수를 추정
반응형
'이론' 카테고리의 다른 글
| [NLP] TF-IDF, Term Freq.-Inverse Document Freq. 개념 정리 (2) | 2025.05.06 |
|---|---|
| [Algorithm] 선형 회귀분석 - Linear Regression Analysis (8) | 2025.04.30 |
| [NLP] 텍스트 임베딩 Text Embedding 개념 정리 - 응용 분야, 종류 (2) | 2025.03.24 |
| [이론] 클러스터링 평가 지표 - ARI, Confusion Matrix (0) | 2025.03.12 |
| [NLP] 코사인 유사도 Cosine Similarity 개념 정리 (4) | 2025.03.05 |