
클러스터링 평가 지표 - ARI, Confusion Matrix
들어가며
클러스터링은 지도 학습과 달리 정답이 없는 경우가 많기 때문에 평가 방법이 모호합니다. 하지만 특정 상황에서는 정답 레이블이 존재하며, 이 때 크러스터링 성능을 객관적으로 평가하는 다양한 지표를 활용할 수 있습니다.
이 글에서는 Adjusted Rand Index(ARI)와 Confusion Matirx(혼동 행렬)을 활용하여 클러스터링 결과를 정량적으로 분석하는 방법을 소개합니다. ARI는 클러스터링 결과와 실제 정답 간의 유사도를 평가하는 지표이며, Confusion Matrix는 예측된 클러스터와 실제 레이블 간의 관계를 시각적으로 나타내는 도구입니다.
- ARI | Adjusted Rand Index
- Confusion Matrix
- ARI와 Confusion Matrix
ARI | Adjusted Rand Index
ARI는 실제 레이블과 클러스터링 결과 간의 유사성을 측정하는 지표로, 일반적인 Rand Index를 보정한 값입니다. 수식은 다음과 같습니다.
$$ ARI = \frac{RI-\mathbb{E}[RI]}{max(RI)-\mathbb{E}[RI]} $$
여기서, $ RI $는 Rand Index, $ \mathbb{E}[RI] $는 무작위 클러스터링일 때의 기대값입니다.
값의 범위는 -1과 1 사이로, 0은 군집한 결과가 랜덤한 경우, 1은 두 군집이 완벽하게 일치하는 경우, 음수는 군집이 무작위보다도 더 나쁜 경우를 의미합니다. 단순 Rand Index와 달리, 기대값을 보정하여 클러스터 개수가 다른 경우에도 공정한 비교가 가능합니다.
| ARI | 결과 |
| 음수 | 우연보다 못한 결과 |
| 0 | 두 군집 간의 유사성 X |
| 1 | 완벽한 군집화 |
RI와 ARI의 차이점
예를 들어, 다음 이미지의 [ 예제 데이터 ]와 같이 4개의 점이 있다고 가정하겠습니다. 점들은 2개의 군집(A,B)로 나뉘어져 있습니다.
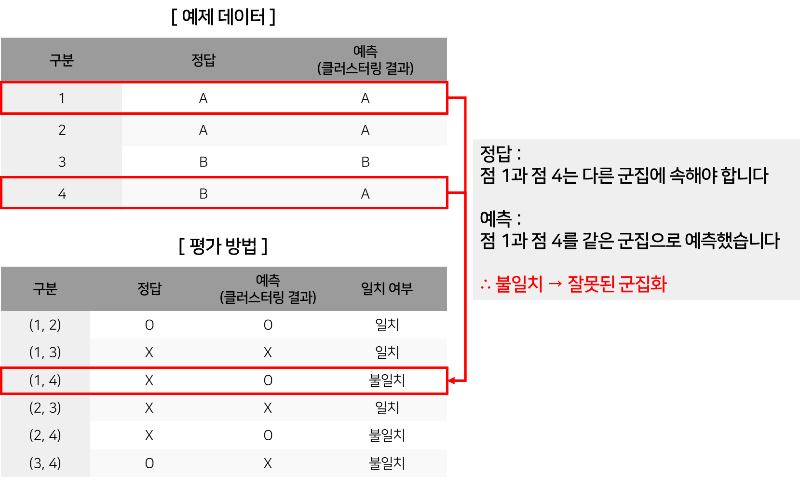
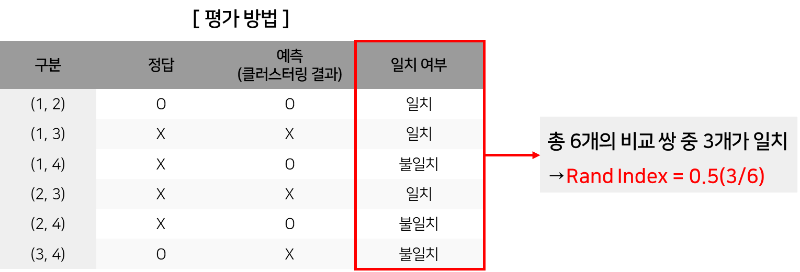
[ 평가 방법 ]에서 2개의 군집을 비교하면, 총 6개의 비교 쌍 중 3개가 일치하는 것을 확인할 수 있습니다. 하지만, 무작위로 클러스터링한 경우에도 비슷한 값이 나올 수 있기 때문에 이를 보정한 값이 ARI입니다.
RI는 단순히 "같은 그룹에 속했는지" 또는 "다른 그룹에 속했는지"를 기준으로 산출하는 지표입니다. 따라서, 데이터를 무작위로 군집화해도, 일정 부분은 우연히 일치할 가능성이 있습니다. 즉, 완전 랜덤한 군집화의 겨웅에도 RI 값이 상대적으로 높게 나오는 단점이 있습니다.
따라서, 위의 ARI 수식과 같이 랜덤하게 군집화한 경우에 나올 수 있는 $ \mathbb{E}[RI] $을 뺀 후, 정규화하는 방식입니다.
파이썬을 활용한 ARI 산출 방법은 다음과 같습니다.
from sklearn.metrics import adjusted_rand_score
labels_true = [0, 0, 1, 1, 2, 2] # 정답
labels_pred = [0, 0, 1, 2, 2, 2] # 클러스터링 결과
ari_score = adjusted_rand_score(labels_true, labels_pred)
print("ARI Score:", ari_score)Confusion Matrix
Confusion Matrix는 클러스터링 외에도 분류 문제에서도 많이 사용되는 지표로 실제 레이블과 예측 레이블 간의 관계를 나타내는 행렬입니다. 주어진 데이터에 대해 모델이 예측한 결과와 실제 정답을 비교하여 4가지 경우의 수를 정리한 표입니다.
TP (True Positive): 실제 값이 Positive(1)인데, 모델이 Positive(1)로 올바르게 예측한 경우
FP (False Positive): 실제 값이 Negative(0)인데, 모델이 Positive(1)로 잘못 예측한 경우 → "Type I Error"
FN (False Negative): 실제 값이 Positive(1)인데, 모델이 Negative(0)로 잘못 예측한 경우 → "Type II Error"
TN (True Negative): 실제 값이 Negative(0)인데, 모델이 Negative(0)로 올바르게 예측한 경우
| 구분 | 실제 1 | Positive | 실제 0 | Negative |
| 예측 1 | Positive | TP(True Positive) | FP(False Positive) |
| 예측 0 | Negative | FN(False Negative) | TN(True Negative) |
파이썬을 활용한 Confusion Matrix 산출 방법은 다음과 같습니다.
from sklearn.metrics import confusion_matrix
import numpy as np
labels_true = [0, 0, 1, 1, 2, 2]
labels_pred = [1, 1, 0, 2, 2, 2] # 클러스터링 결과
cm = confusion_matrix(labels_true, labels_pred)
print("Confusion Matrix:\n", cm)ARI와 Confusion Matrix
ARI와 Confusion Matrix를 함께 활용하면, 클러스터링의 정확성을 더 깊이 있게 분석할 수 있습니다.
ARI:
클러스터링 성능을 평가하는 지표. 무작위 클러스터링과 비교하여 얼마나 나은지를 보여주는 지표
Confusion Matrix:
클러스터링된 개체(데이터 포인트)가 원래 군집(Ground Truth)과 비교하여 어디로 이동했는지를 보여주는 행렬
즉, ARI는 군집화의 전반적인 품질을 하나의 값으로 요약하며, Confusion Matrix는 세부적으로 어떤 군집에서 오류가 발생했는지 분석이 가능한 지표입니다.
예를 들어, ARI와 Confusion Matrix를 함께 활용하는 방법은 다음과 같습니다.
특정 클러스터링에 대한 ARI 값이 0.72가 나왔을 때, "클러스터링이 꽤 정확하지만, 일부 오차가 있음"이라고 판단할 수 있습니다. 따라서 ARI 값만으로는 어느 군집에서 문제가 발생했는지를 알기 어렵기에 Confusion Matrix가 필요합니다.

위의 Confusion Matrix 결과를 통해 다음과 같은 해석을 할 수 있습니다.
1. 클러스터 1은 대부분 잘 맞음(45/50 개)
2. 클러스터 2에서 일부 데이터(7개)가 클러스터 3으로 잘못 분류됨
3. 클러스터 3에서도 8개의 데이터가 클러스터 2로 이동함 → 혼동 발생
이와 같이 ARI로 "군집화가 괜찮다"는 결론을 얻었다면, Confusion Matrix로 "어떤 군집에서 오류가 있는지"를 알 수 있습니다.
'이론' 카테고리의 다른 글
| [Algorithm] 회귀 분석 - Regression Analysis (0) | 2025.04.19 |
|---|---|
| [NLP] 텍스트 임베딩 Text Embedding 개념 정리 - 응용 분야, 종류 (2) | 2025.03.24 |
| [NLP] 코사인 유사도 Cosine Similarity 개념 정리 (4) | 2025.03.05 |
| [NLP] 자연어 처리 입문을 위한 개념 정리- NLP, LLM (3) | 2025.02.17 |
| [NLP] 자카드 유사도 Jaccard Similarity 개념 정리 (4) | 2025.02.13 |