
중심극한정리 Central Limit Theorem, CLT에 대하여
중심극한정리란?
중심극한정리는 확률론과 통계학에서 중요한 이론 중 하나로, "표본의 평균이 정규분포에 가까워진다"는 사실을 설명합니다.
중심극한정리란,
"표본의 크기가 충분히 크면, 표본평균의 분포는 정규분포에 수렴한다"
는 통계학의 핵심 이론입니다.
예를 들어, '동전 던지기'에서 동전을 1번 던질 때 앞면이 나올 확률은 0.5(이항분포)입니다. 하지만, 동전을 100번 던져서 앞면이 나온 비율을 기록하고, 이 실험을 여러 번 반복하면 그 결과는 점점 정규분포 곡선에 가까워집니다.
즉, 개별 사건은 이항 분포를 따르지만, 그 평균의 분포는 정규분포에 수렴하게 되는 것을 '중심극한정리'라고 합니다.
중심극한정리가 중요한 이유
중심극한정리는 통계 추론의 기초입니다. 실제 데이터가 정규분포가 아니어도, 충분히 큰 표본을 사용하면 정규분포 기반의 통계추론을 적용할 수 있습니다.
| 활용 분야 | 설명 |
| 표본 추정 | 표본평균을 이용해 모집단의 평균을 추정할 수 있습니다. |
| 신뢰구간 계산 | 표본평균이 정규분포를 따른다고 가정하고 계산합니다. |
| 가설검정 | 표본 통계량의 분포를 정규분포로 근사하여 검정 통계량을 계산합니다. |
수학적 정의
모집단의 평균을 $\mu$, 분산을 $\sigma ^{2}$이라고 할 때, 크기가 $n$인 표본을 여러 번 추출해 각 표본의 평균을 구하는 수식은 다음과 같습니다.
$$ \overline{X} = \frac{1}{n}\sum_{i=1}^{n}X_{i} $$
위의 표본평균의 분포는 다음과 같습니다.
$$ \overline{X} \sim N(\mu ,\frac{\sigma ^{2}}{n}) $$
즉, 표본의 수가 많아질수록(=$n$이 커질수록), 분포의 모양은 점점 정규분포에 가까워지고, 분산은 $\frac{\sigma ^{2}}{n}$으로 줄어듭니다.
시각화를 활용한 중심극한정리 이해
지수분포를 예로 표본 크기($n$)이 1, 5, 30, 100에서 표본평균의 분포가 정규분포에 가까워지는 과정을 시각화하면 다음과 같습니다.
지수분포는 매우 비대칭적이고, 꼬리가 긴 분포입니다. 하지만, $n$의 값이 증가할수록 정규분포의 형태와 비슷하고, $n$이 100인 경우에는 완전히 정규분포와 거의 일치합니다. 정규분포가 아니어도, 표본평균의 분포는 정규분포로 수렴한다는 것을 시각화를 통해 이해할 수 있습니다.
$n=1$

$n=5$
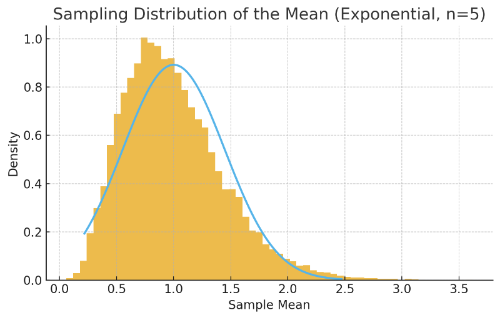
$n=30$
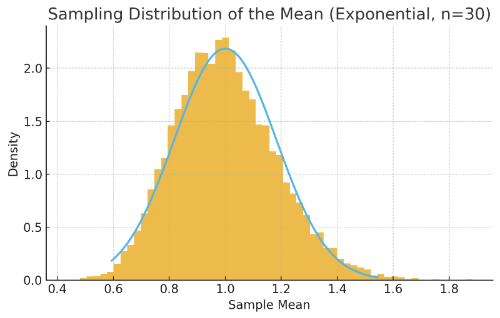
$n=100$

'이론' 카테고리의 다른 글
| [통계] 여론조사 속 통계(신뢰 수준, 표본오차) 개념 정리 (3) | 2025.12.22 |
|---|---|
| [검색] 키워드 서치, 시맨틱 서치, 하이브리드 서치 개념 정리 (2) | 2025.11.17 |
| [LLM] 토큰 Token에 대하여 - 모델이 언어를 이해하는 최소 단위 (2) | 2025.11.02 |
| [NLP] TF-IDF, Term Freq.-Inverse Document Freq. 개념 정리 (2) | 2025.05.06 |
| [Algorithm] 선형 회귀분석 - Linear Regression Analysis (8) | 2025.04.30 |