
텐서의 개념
들어가며
이 글에서는 머신러닝의 기본 구성 요소인 텐서에 대해 설명합니다. 구글이 개발한 오픈소스 딥러닝 라이브러리인 텐서플로 이름 또한 Tensor(텐서)와 Flow(데이터의 흐름)이라는 의미를 담고 있습니다. 이 글에서는 텐서의 종류를 중점적으로 소개합니다.
텐서는 데이터를 위한 컨테이너로 다차원 넘파이 배열입니다. 텐서는 축의 개수를 기준으로 다음 표와 같이 랭크-0, 랭크-1 등으로 나누어집니다. 보통 랭크 0에서 4까지의 텐서를 다루지만, 동영상은 랭크-5 텐서까지 다루기도 합니다. 각각의 텐서에 대한 자세한 내용은 아래 글에서 이어집니다.
| 축의 개수 | 구분 |
| 0 | 랭크-0 텐서, 스칼라 |
| 1 | 랭크-1 텐서, 벡터 |
| 2 | 랭크-2 텐서, 행렬 |
| 3 | 랭크-3 텐서 |
| 4 | 랭크-4 텐서 |
| 5 | 랭크-5 텐서 |
- 랭크-0 텐서
- 랭크-1 텐서
- 랭크-2 텐서
- 랭크-3 텐서
랭크-0 텐서
다음과 같이 하나의 숫자만을 담고있는 x 배열을 생성하고, ndim을 활용하여 넘파이 배열의 축 개수를 확인하겠습니다. x는 오직 1개의 숫자인 12를 배열로 갖고 있습니다.
x.ndim으로 확인한 x의 넘파이 배열의 축 개수는 0개입니다. 이를 랭크-0 텐서, 스칼라라고 합니다.
import numpy as np
x = np.array(12)
print('x: ',x)
print('ndim: ',x.ndim)
랭크-1 텐서
다음과 같이 여러 개의 숫자를 담고 있는 x1 배열을 생성하고, ndim을 활용하여 넘파이 배열의 축 개수를 확인하겠습니다. x1는 4개의 숫자들을 배열로 갖고 있습니다.
x1.ndim으로 확인한 x1의 넘파이 배열의 축 개수는 1개입니다. 이를 랭크-1 텐서, 벡터라고 합니다. 또한, x1 벡터는 4개의 원소를 갖고 있기 때문에 4차원 벡터입니다. ** 여기서 주의할 점은 4차원 벡터와 4차원 텐서를 혼동하면 안 됩니다. 4차원 벡터(4개의 차원)와 4차원 텐서(4개의 축)는 다른 개념입니다.
x1 = np.array([12,3,6,7])
print('x1: ',x1)
print('ndim: ',x1.ndim)
랭크-2 텐서
다음과 같이 x2 배열을 생성하고, ndim을 활용하여 넘파이 배열의 축 개수를 확인하겠습니다. 아래 그림과 같이 x2는 3개의 행과 2개의 열을 가진 배열입니다.
x2 = np.array([[5,78,2,34,0],
[6,79,3,35,1],
[7,80,4,36,2]])
x2

x2.ndim으로 확인한 x2의 넘파이 배열의 축 개수는 2개입니다. 이를 랭크-2 텐서, 행렬이라고 합니다.
print('ndim: ',x2.ndim)
랭크-3 텐서
위의 랭크-2 텐서인 행렬들을 하나의 새로운 배열로 합치면 랭크-3 텐서를 생성할 수 있습니다. 다음과 같이 x3 배열을 생성하고, ndim을 활용하여 넘파이 배열의 축 개수를 확인하겠습니다.
x3 = np.array([[[5,78,2,34,0],
[6,79,3,35,1],
[7,80,4,36,2]],
[[5,78,2,34,0],
[6,79,3,35,1],
[7,80,4,36,2]],
[[5,78,2,34,0],
[6,79,3,35,1],
[7,80,4,36,2]]])
x3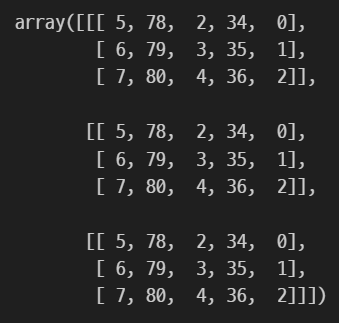
print('ndim: ',x3.ndim)
참고 도서:
케라스 창시자에게 배우는 딥러닝
'이론' 카테고리의 다른 글
| [NLP] 자연어 처리 입문을 위한 개념 정리- NLP, LLM (3) | 2025.02.17 |
|---|---|
| [NLP] 자카드 유사도 Jaccard Similarity 개념 정리 (4) | 2025.02.13 |
| [DL] 딥러닝의 작동 원리 - 가중치, 손실함수, 옵티마이저를 중심으로 (0) | 2024.12.23 |
| [ML/DL] 데이터 전처리 - Z-Score 표준화 Standardization 개념 (3) | 2024.12.20 |
| [Algorithm] 선형 회귀분석 - Linear Regression Analysis (4) | 2024.09.12 |